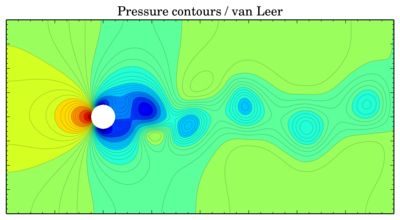
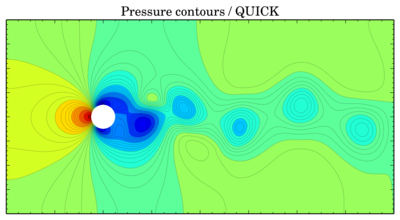
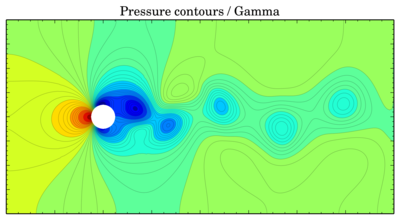
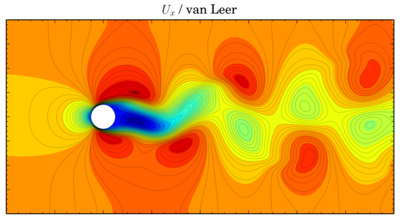
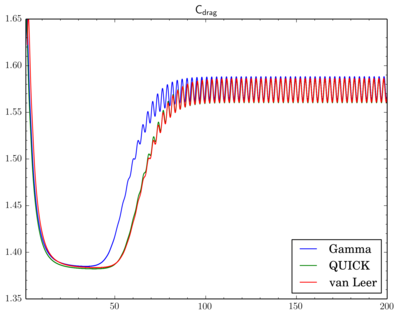
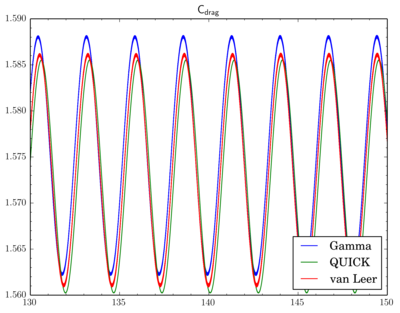
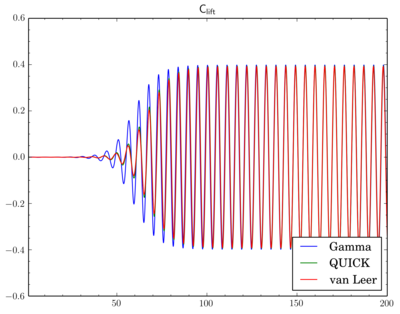
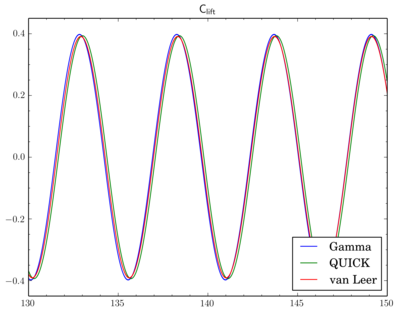
NB. Updated versions of the patches are on Github.
Previous patches I've posted in this blog (
#1,
#2,
#3) have certain mistakes. Mainly because I forgot about
DYLD_LIBRARY_PATH environment variable and did not test parallel execution of the solvers. Recently I've decided it is time to fix it. Also that tiny feedback I had, showed that there is two common errors during compilation: people create disk images with case insensitive file system and they try to apply patches in an arbitrary folders. The second problem is hard to solve by a blog post, while the first one can be solved if we change the process of disk image creation. Go from error-prone GUI way to just one command executed in terminal window. And here goes the guide.
Build process was tested on OS X version 10.9.2 with
clang --version: Apple LLVM version 5.1 (clang-503.0.38) (based on LLVM 3.4svn).
Before we start
I've made certain assumptions about the software you have on your Mac:
- Homebrew is used as a package manager to install open source software. If not, you can install it following instructions on the site.
- All software from ThirdParty source pack will be installed using Homebrew.
- All commands are executed in Terminal application (usually it is called Terminal.app).
$ in the beginning of the lines is a shell prompt and you don't need to copy it, if you're copy/pasting commands from the post. In general commands should be executed in the sequence shown in the post.- You've downloaded Paraview application from paraview.org and installed it in /Applications.
To install dependencies you can use the following set of commands:
$ brew tap homebrew/science
$ brew install open-mpi
$ brew install scotch
$ brew install boost --without-single --with-mpi
$ brew install cgal
The last command will also install
cmake,
gmp, and
mpfr as dependencies.
Downloading necessary pieces
At this point it is time to decide what version of OpenFOAM you'd like to build. As 2.3.0 introduced certain backward incompatible changes, I've made patches for 2.2.2 and 2.3.0. Further in the guide I assume you've downloaded source pack and patch into
~/Downloads/OpenFOAM folder.
OpenFOAM 2.2.2
Download source pack. Either following link on the OpenFOAM web site
http://www.openfoam.org/archive/2.2.2/download/source.php, or by executing the following commands in in Terminal:
$ cd Downloads
$ mkdir OpenFOAM && cd OpenFOAM
$ curl -L http://downloads.sourceforge.net/foam/OpenFOAM-2.2.2.tgz > OpenFOAM-2.2.2.tgz
Download patch using following link
https://raw.githubusercontent.com/mrklein/openfoam-os-x/master/OpenFOAM-2.2.2.patch, or if you still have terminal opened, issue the command:
$ curl -L https://raw.githubusercontent.com/mrklein/openfoam-os-x/master/OpenFOAM-2.2.2.patch > OpenFOAM-2.2.2.patch
OpenFOAM 2.3.0
Download source pack. Either following link on the OpenFOAM web site -
http://www.openfoam.org/download/source.php, or just executing this in Terminal:
$ cd Downloads
$ mkdir OpenFOAM && cd OpenFOAM
$ curl -L http://downloads.sourceforge.net/foam/OpenFOAM-2.3.0.tgz > OpenFOAM-2.3.0.tgz
Download patch using following link
https://raw.githubusercontent.com/mrklein/openfoam-os-x/master/OpenFOAM-2.3.0.patch, or if you still have terminal opened issue the command:
$ curl -L https://raw.githubusercontent.com/mrklein/openfoam-os-x/master/OpenFOAM-2.3.0.patch > OpenFOAM-2.3.0.patch
After this you're ready to proceed to the actual build process.
Building OpenFOAM
!!! Cause certain file names in this part depend on the version of OpenFOAM you're building, I use N and M variables in the file names. For OpenFOAM version 2.2.2: N=2, M=2; for OpenFOAM version 2.3.0: N=3, M=0.
Also it is possible that you already have disk image with the same name in your home folder. Correct the names accordingly.
To build OpenFOAM first you need to create disk image with case sensitive file system. You can either follow the guide from
OpenFOAM wiki, or just issue these commands in your terminal:
$ cd
$ hdiutil create -size 4.4g -type SPARSEBUNDLE -fs HFSX -volname OpenFOAM -fsargs -s OpenFOAM.sparsebundle
Last command will create disk image with the name OpenFOAM.sparsebundle with estimated size 4.4 G (as it is the sparse image, after creation the size of the file will be different), create HFS+ file system with a volume name OpenFOAM in the image. Finally
-fsargs -s will instruct
newfs_hfs utility to create case sensitive file system.
After the image was created you can mount it, I will assume it is mounted in $HOME/OpenFOAM
$ mkdir OpenFOAM
$ hdiutil attach -mountpoint $HOME/OpenFOAM OpenFOAM.sparsebundle
After you extract source pack, copy patch to the created folder, and apply patch (remember, you've downloaded the source pack and the patch into
~/Downloads/OpenFOAM):
$ cd OpenFOAM
$ tar xzf ~/Downloads/OpenFOAM/OpenFOAM-2.N.M.tgz
$ cd OpenFOAM-2.N.M
$ cp ~/Downloads/OpenFOAM/OpenFOAM-2.N.M.patch .
$ git apply OpenFOAM-2.N.M.patch
At this point maybe you'll need to edit
etc/bashrc file. But since compiler settings are fixed (it is Clang), OpenMPI and other libraries settings are fixed (they are installed with Homebrew), in fact the only thing worth editing is path settings and only in case if you're installing OpenFOAM elsewhere (i.e. not in $HOME/OpenFOAM). Now you're more-or-less ready to compile.
$ source etc/bashrc
$ ./Allwmake > log.Allwmake 2>&1
The last command executes
Allwmake script and redirects its output to
log.Allwmake file; just in case, if anything goes wrong, it'll be easy to locate the source of error having this log file.
After Allwmake execution is finished, you can test the build with:
$ mkdir -p $FOAM_RUN
$ run
$ cp -r $FOAM_TUTORIALS/incompressible/icoFoam/cavity .
$ cd cavity
$ blockMesh
$ icoFoam
If you'd like to test parallel run, it is necessary to do:
$ cat > system/decomposeParDict
/*--------------------------------*- C++ -*----------------------------------*\
| ========= | |
| \\ / F ield | OpenFOAM: The Open Source CFD Toolbox |
| \\ / O peration | Version: 2.3.0 |
| \\ / A nd | Web: www.OpenFOAM.org |
| \\/ M anipulation | |
\*---------------------------------------------------------------------------*/
FoamFile
{
version 2.0;
format ascii;
class dictionary;
location "system";
object decomposeParDict;
}
// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //
numberOfSubdomains 4;
method scotch;
^D
$ decomposePar
$ mpiexec -np 4 icoFoam -parallel
(
^D is entered with Ctrl and D keys pressed together)
Post-configuration
There are several ways of managing mounting disk image and sourcing
etc/bashrc file.
The first one is to define alias in your
$HOME/.profile:
alias of2NM='hdiutil attach -quiet -mountpoint $HOME/OpenFOAM OpenFOAM.sparsebundle; sleep 1; source $HOME/OpenFOAM/OpenFOAM-2.N.M/etc/bashrc'
The second one is to create
$HOME/.OpenFOAM-release file with a version of OpenFOAM you'd like to use:
$ echo '2.N.M' > $HOME/.OpenFOAM-release
and then add the following lines to your
$HOME/.profile:
if [ -f $HOME/.OpenFOAM-release ]; then
OF_VER=$(cat $HOME/.OpenFOAM-release)
if [ ! -f $HOME/OpenFOAM/OpenFOAM-$OF_VER/etc/bashrc ]; then
hdiutil attach -quiet -mountpoint $HOME/OpenFOAM OpenFOAM.sparsebundle && . $HOME/OpenFOAM/OpenFOAM-$OF_VER/etc/bashrc
else
. $HOME/OpenFOAM/OpenFOAM-$OF_VER/etc/bashrc
fi
fi
And finally third one is to transform second version in the set of functions. I.e. instead of automatic attachment of disk image upon terminal start, you'll need to execute function which will mount necessary disk image and source bashrc:
of2xx() {
local version=$1
if [ ! -f $HOME/OpenFOAM/OpenFOAM-$version/etc/bashrc ]; then
hdiutil attach -quiet -mountpoint $HOME/OpenFOAM OpenFOAM.sparsebundle &&
. $HOME/OpenFOAM/OpenFOAM-$version/etc/bashrc
else
. $HOME/OpenFOAM/OpenFOAM-$version/etc/bashrc
fi
}
of2NM() {
of2xx '2.N.M'
}
Add this code to your $HOME/.profile and use of2NM command to setup environment.
And that's it.