Building hexagonal meshes with Gmsh

OpenFOAM's blockMesh is rather simple and efficient way of building meshes but it has certain annoying features:

1. Entities numbering. To construct a block, an edge or a boundary one has to know its vertices numbers, they are numbered automatically stating with 0. So while constructing a mesh one can, for example, use vim with +relativenumber and blockMeshDict opened in two splits (see screenshot). But when blockMesh reports about errors in the mesh description it also uses these automatic numbers of entities. Soon it becomes rather annoying to look for the block #4 or #17 to correct gradings or densities.
2. Mesh grading is a good thing but for example to make a cube mesh with a higher density near the walls, one has to cut the cube into 4 blocks and make consistent grading in each block.
3. Curved edges is something special. For a 2D case it's rather simple to make an utility to calculate coordinates of a point on the arc of a given radius passing through two vertices, in a 3D case it's less obvious.
4. And finally workflow vim -> blockMesh -> paraFoam is rather slow.

Gmsh usually used with the finite-element code GetDP so by default it generates tetrahedral meshes, like one below.

But it is possible to make hexagonal meshes with it. All GEO files from the sections below can be found in the repository.

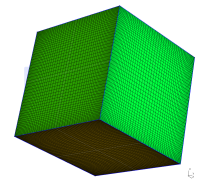
Cube

To make a cube one has to create 8 vertices (with Gmsh's GUI, for example, but in fact it's simpler to create the points in an editor):

// Syntax.: Point(n) = {x, y, z, hs};
// As we'll use transfinite algorithm hs can be arbitrary
// or even omitted from mesh description
Point(1) = {0, 0, 0, 1.0};
Point(2) = {1, 0, 0, 1.0};
Point(3) = {0, 1, 0, 1.0};
Point(4) = {1, 1, 0, 1.0};
Point(5) = {1, 1, 1, 1.0};
Point(6) = {1, 0, 1, 1.0};
Point(7) = {0, 1, 1, 1.0};
Point(8) = {0, 0, 1, 1.0};

connect them with lines

Line(1) = {3, 7};
Line(2) = {7, 5};
Line(3) = {5, 4};
Line(4) = {4, 3};
Line(5) = {3, 1};
Line(6) = {2, 4};
Line(7) = {2, 6};
Line(8) = {6, 8};
Line(9) = {8, 1};
Line(10) = {1, 2};
Line(11) = {8, 7};
Line(12) = {6, 5};

and that's it, we have a cube.

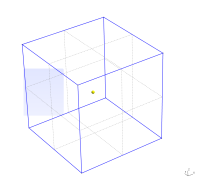
Surely after to create real 3D mesh one has to define its boundary plane

Line Loop(13) = {7, 8, 9, 10};
Plane Surface(14) = {13};
Line Loop(15) = {6, 4, 5, 10};
Plane Surface(16) = {15};
Line Loop(17) = {3, 4, 1, 2};
Plane Surface(18) = {17};
Line Loop(19) = {12, -2, -11, -8};
Plane Surface(20) = {19};
Line Loop(21) = {7, 12, 3, -6};
Plane Surface(22) = {21};
Line Loop(23) = {9, -5, 1, -11};
Plane Surface(24) = {23};
Surface Loop(25) = {14, 22, 20, 18, 16, 24};

and volume

Volume(26) = {25};

And the next lines will convert default generation strategy from tetrahedral meshes to hexagonal

Transfinite Line "*" = 100 Using Bump 0.25;
Transfinite Surface "*";
Recombine Surface "*";
Transfinite Volume "*";

As the lengths of the cube sides are equal, densities of the 1D mesh on every side are equal (also I've used keyword Bump to grade the mesh near the corners). To use generated mesh in OpenFOAM one has to define physical groups also:

Physical Surface("top") = {20};
Physical Surface("bottom") = {16};
Physical Surface("sides") = {14, 24, 18, 22};
Physical Volume("cube") = {26};

Et voila, we've got graded hexagonal mesh of a cube:

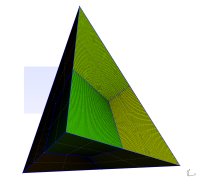
Tetrahedron

This mesh is less trivial than the previous one, the idea of a tetrahedron cut is taken from the article by David Eppstein. Let's assume tetrahedron with the following corners: (-5, 0, -5), (5, 0, -5) and (0, -5, 5), (0, 5, 5). To decompose the tetrahedron into 6-faced volumes one needs to know centers of the sides, centers of the faces and center of the tetrahedron:

Point(1) = {-5, 0, -5, 1.0};
Point(2) = {5, 0, -5, 1.0};
Point(3) = {0, -5, 5, 1.0};
Point(4) = {0, 5, 5, 1.0};
Point(5) = {0, 0, 0, 1.0};
Point(6) = {0, 0, -5, 1.0};
Point(7) = {0, 0, 5, 1.0};
Point(8) = {-2.5, -2.5, 0, 1.0};
Point(9) = {-2.5, 2.5, 0, 1.0};
Point(10) = {2.5, -2.5, 0, 1.0};
Point(11) = {-2.5, 2.5, 0, 1.0};
Point(12) = {2.5, 2.5, 0, 1.0};
Point(13) = {0, 1.66666667, -1.66666667, 1.0};
Point(14) = {0, -1.66666667, -1.66666667, 1.0};
Point(15) = {-1.66666667, 0, 1.66666667, 1.0};
Point(16) = {1.66666667, 0, 1.66666667, 1.0};

After connection of the points with the lines, defining faces and volumes, we get the following geometry:

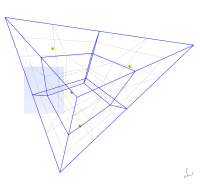
As the densities of the different parts of the mesh should be more or less the same one can add the same four lines as with the cube to have hexagonal mesh

Transfinite Line "*" = 60;
Transfinite Surface "*";
Recombine Surface "*";
Transfinite Volume "*";

and the final mesh will be like this

One of the characteristics of the mesh one should check before running a simulation is non-orthogonality (I omitted this step in case of cube as obviously for that case non-orthogonality is 0). Here is the report of the checkMesh utility for the generated mesh:

Checking geometry...
    Overall domain bounding box (-5 -5 -5) (5 5 5)
    Mesh (non-empty, non-wedge) directions (1 1 1)
    Mesh (non-empty) directions (1 1 1)
    Boundary openness (1.67777e-16 -6.72996e-16 1.01043e-15) OK.
    Max cell openness = 2.87305e-16 OK.
    Max aspect ratio = 2.93743 OK.
    Minimum face area = 0.00139386. Maximum face area = 0.00798479.  Face area magnitudes OK.
    Min volume = 4.6248e-05. Max volume = 0.000598376.  Total volume = 166.667.  Cell volumes OK.
    Mesh non-orthogonality Max: 44.2633 average: 22.1599
    Non-orthogonality check OK.
    Face pyramids OK.
    Max skewness = 0.590514 OK.
    Coupled point location match (average 0) OK.

Mesh OK.

One can play with the points positions to get more orthogonal mesh but 44 is not so bad.

Cylinder

Trivial solution when one just take a cube and turn it into a cylinder by specifying certain sides as the arcs leads to the highly non-orthogonal meshes. Surely there're many ways to build mesh on a cylinder, below are several variants.

Version 1

Top view of the cylinder subdivision looks like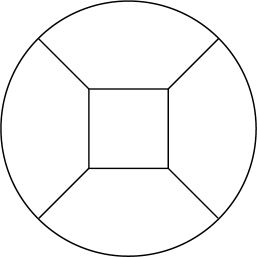

it is a square inside a circle. So we need 9 points (4 for the square, 4 on the circle and one for the center of the arcs) in each horizontal plane.

Point(1) = {0, 0, 0, 1.0};
Point(2) = {3.5355339059327373, 3.5355339059327373, 0, 1.0};
Point(3) = {7.0710678118654746, 7.0710678118654746, 0, 1.0};
Point(4) = {-3.5355339059327373, 3.5355339059327373, 0, 1.0};
Point(5) = {-7.0710678118654746, 7.0710678118654746, 0, 1.0};
Point(6) = {-3.5355339059327373, -3.5355339059327373, 0, 1.0};
Point(7) = {-7.0710678118654746, -7.0710678118654746, 0, 1.0};
Point(8) = {3.5355339059327373, -3.5355339059327373, 0, 1.0};
Point(9) = {7.0710678118654746, -7.0710678118654746, 0, 1.0};
Point(10) = {0, 0, 12.42, 1.0};
Point(11) = {3.5355339059327373, 3.5355339059327373, 12.42, 1.0};
Point(12) = {7.0710678118654746, 7.0710678118654746, 12.42, 1.0};
Point(13) = {-3.5355339059327373, 3.5355339059327373, 12.42, 1.0};
Point(14) = {-7.0710678118654746, 7.0710678118654746, 12.42, 1.0};
Point(15) = {-3.5355339059327373, -3.5355339059327373, 12.42, 1.0};
Point(16) = {-7.0710678118654746, -7.0710678118654746, 12.42, 1.0};
Point(17) = {3.5355339059327373, -3.5355339059327373, 12.42, 1.0};
Point(18) = {7.0710678118654746, -7.0710678118654746, 12.42, 1.0};

Alternatively we can start only with 9 points in one plane and then use extrude operation. After connection of the points with lines and arcs, defining planes and volumes cylinder geometry will look like

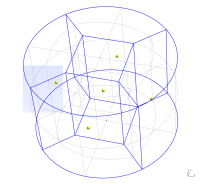
3 set of lines can have independent 1D mesh densities, so we define them

// Lines of the square and arcs of the circle
Transfinite Line {1, 2, 3, 4} = 60;
Transfinite Line {17, 18, 19, 20} = 60;
Transfinite Line {9, 10, 11, 12} = 60;
Transfinite Line {21, 22, 23, 24} = 60;

// Lines connecting square and circle
Transfinite Line {5, 6, 7, 8, 13, 14, 15, 16} = 60;

// Vertical lines
Transfinite Line {31, 32, 29, 30, 27, 28, 25, 26} = 61;

as usual all planes and volumes will be meshed with transfinite algorithm

Transfinite Surface "*";
Recombine Surface "*";
Transfinite Volume "*";

Finally we'll have this mesh

Below is the output of the checkMesh utility, 42 as a maximum value of non-orthogonality is not catastrophic but I'll try to improve it.

Checking geometry...
    Overall domain bounding box (-9.99911 -9.99911 0) (9.99911 9.99911 12.42)
    Mesh (non-empty, non-wedge) directions (1 1 1)
    Mesh (non-empty) directions (1 1 1)
    Boundary openness (4.94158e-16 -1.11872e-17 -2.57076e-15) OK.
    Max cell openness = 2.46233e-16 OK.
    Max aspect ratio = 4.96072 OK.
    Minimum face area = 0.00750141. Maximum face area = 0.0551113.  Face area magnitudes OK.
    Min volume = 0.00155279. Max volume = 0.00600909.  Total volume = 3901.4.  Cell volumes OK.
    Mesh non-orthogonality Max: 42.4768 average: 7.66228
    Non-orthogonality check OK.
    Face pyramids OK.
    Max skewness = 0.994206 OK.
    Coupled point location match (average 0) OK.

Mesh OK.

Version 2

The first idea that comes to mind in the quest for reducing non-orthogonality of the mesh is to use a square with the curved sides. Let them be arcs with a radius R_sq < R_cyl. Schematic top view of the cylinder division will look like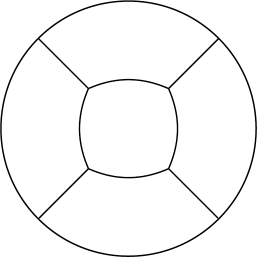

To have curved sides of the square we need to define additional points which will be the centers of the circle arcs

Point(19) = {5.5355339059327373, 0, 0, 1.0};
Point(20) = {-5.5355339059327373, 0, 0, 1.0};
Point(21) = {0, 5.5355339059327373, 0, 1.0};
Point(22) = {0, -5.5355339059327373, 0, 1.0};
Point(23) = {5.5355339059327373, 0, 12.42, 1.0};
Point(24) = {-5.5355339059327373, 0, 12.42, 1.0};
Point(25) = {0, 5.5355339059327373, 12.42, 1.0};
Point(26) = {0, -5.5355339059327373, 12.42, 1.0};

As usual we need to define all the lines connecting points, then planes, and finally volumes. Geometry will look like this

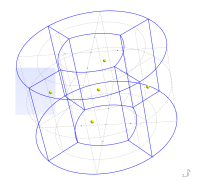
You can see those additional points which are the centers of the circle arcs of the "square" sides. Definition of the entities for transfinite meshing algorithm is almost the same as for the previous case. And here is the mesh

As the selection of the radius for the "square" arcs was more or less arbitrary we got a mesh with higher non-orthogonality:

Checking geometry...
    Overall domain bounding box (-9.99911 -9.99911 0) (9.99911 9.99911 12.42)
    Mesh (non-empty, non-wedge) directions (1 1 1)
    Mesh (non-empty) directions (1 1 1)
    Boundary openness (8.35962e-18 -1.03744e-17 3.99587e-16) OK.
    Max cell openness = 2.56391e-16 OK.
    Max aspect ratio = 3.5246 OK.
    Minimum face area = 0.00976445. Maximum face area = 0.0551113.  Face area magnitudes OK.
    Min volume = 0.00202124. Max volume = 0.00523421.  Total volume = 3901.4.  Cell volumes OK.
    Mesh non-orthogonality Max: 50.0779 average: 6.73459
    Non-orthogonality check OK.
    Face pyramids OK.
    Max skewness = 0.504102 OK.
    Coupled point location match (average 0) OK.

Mesh OK.

Though the mesh is OK we'll make another mesh in the quest for the lower non-orthogonality.

Version 3

This time we'll convert the square into an octagon to gain control over additional points. Schematic top view of the cylinder subdivision will look like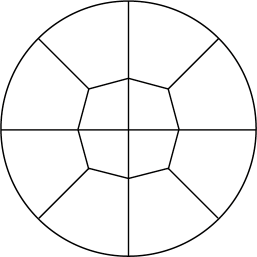

So in addition to 18 points of the first subdivision scheme we get 16 more points

Point(19) = {4.4505974153938341, 0, 0, 1.0};
Point(20) = {-4.4505974153938341, 0, 0, 1.0};
Point(21) = {0, 4.4505974153938341, 0, 1.0};
Point(22) = {0, -4.4505974153938341, 0, 1.0};
Point(23) = {4.4505974153938341, 0, 12.42, 1.0};
Point(24) = {-4.4505974153938341, 0, 12.42, 1.0};
Point(25) = {0, 4.4505974153938341, 12.42, 1.0};
Point(26) = {0, -4.4505974153938341, 12.42, 1.0};

Point(27) = {10, 0, 0, 1.0};
Point(28) = {-10, 0, 0, 1.0};
Point(29) = {0, 10, 0, 1.0};
Point(30) = {0, -10, 0, 1.0};
Point(31) = {10, 0, 12.42, 1.0};
Point(32) = {-10, 0, 12.42, 1.0};
Point(33) = {0, 10, 12.42, 1.0};
Point(34) = {0, -10, 12.42, 1.0};

After definition of the lines, planes and volumes we'll get the following geometry

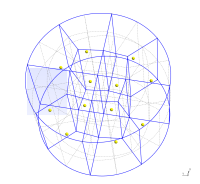
Mesh looks like this

checkMesh output is show below and this will be the final version of the mesh.

Checking geometry...
    Overall domain bounding box (-10 -10 0) (10 10 12.42)
    Mesh (non-empty, non-wedge) directions (1 1 1)
    Mesh (non-empty) directions (1 1 1)
    Boundary openness (-5.92258e-17 1.42868e-16 1.79229e-15) OK.
    Max cell openness = 2.91797e-16 OK.
    Max aspect ratio = 3.98032 OK.
    Minimum face area = 0.00945675. Maximum face area = 0.0560611.  Face area magnitudes OK.
    Min volume = 0.00195755. Max volume = 0.00538261.  Total volume = 3901.38.  Cell volumes OK.
    Mesh non-orthogonality Max: 28.5444 average: 7.10033
    Non-orthogonality check OK.
    Face pyramids OK.
    Max skewness = 0.74746 OK.
    Coupled point location match (average 0) OK.

Mesh OK.

Spherical cap

Spherical cap meshing is a further development of the last variant of cylinder mesh. Schematic top and center-plane cut views of the geometry decomposition are shown below, top view is the same as for cylinder and center-plane cut is almost the same as a half of top view.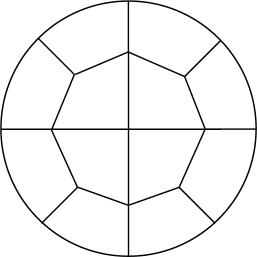


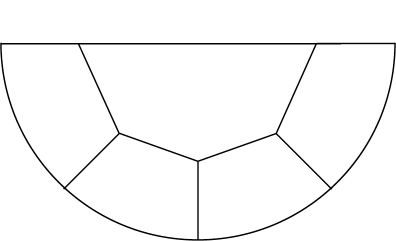
As the number of points in subdivision grows now it's easier to generate points programmatically than by hand. This is especially true for the points inside the cap and on "bottom" of the sphere. Still to connect points and to create the planes and the volumes one can use GUI (though it becomes less and less convenient). After these operations one get the following spherical cap decomposition into hexagonal volumes

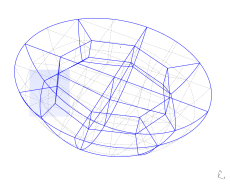
In this case we have three sets of lines which can have different 1D mesh densities

density1 = 40;
density2 = 60;
density3 = 60;

// Vertical lines and arcs
Transfinite Line {122, 41, 42, 43, 44, 45, 46, 47, 48} = density1;
Transfinite Line {58, 59, 60, 61, 62, 63, 64, 65} = density1;

Transfinite Line {9, 10, 11, 14, 39, 30, 31, 32} = density2;
Transfinite Line {1, 2, 7, 12, 13, 17, 18, 6} = density2;
Transfinite Line {33, 34, 35, 36, 37, 38, 39, 40} = density2;
Transfinite Line {21, 22, 23, 24, 25, 26, 27, 28, 29} = density2;
Transfinite Line {66, 67, 68, 69, 70, 71, 72, 73} = density2;
Transfinite Line {74, 75, 76, 77} = density2;

Transfinite Line {49, 56, 16, 57, 15, 50, 8, 51} = density3;
Transfinite Line {4, 52, 3, 53, 5, 54, 19, 55, 20} = density3;

Transfinite Surface "*";
Recombine Surface "*";

Transfinite Volume "*";

And so after meshing spherical cap looks likes this

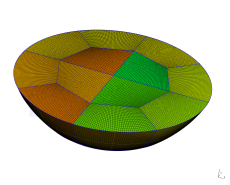
checkMesh report again indicates that we can improve our mesh, in general, it can be achieved by playing with points displacements in the top plane and especially by playing with the angles between octagonal cylindroid and points at the "bottom" of the cap.

Checking geometry...
    Overall domain bounding box (-6.25 -6.25 0) (6.25 6.25 4.4)
    Mesh (non-empty, non-wedge) directions (1 1 1)
    Mesh (non-empty) directions (1 1 1)
    Boundary openness (-5.1934e-17 -2.24174e-16 -3.86814e-15) OK.
    Max cell openness = 3.41873e-16 OK.
    Max aspect ratio = 3.10774 OK.
    Minimum face area = 0.000937704. Maximum face area = 0.00877925.  Face area magnitudes OK.
    Min volume = 3.14526e-05. Max volume = 0.000443903.  Total volume = 311.72.  Cell volumes OK.
    Mesh non-orthogonality Max: 46.0019 average: 13.8361
    Non-orthogonality check OK.
    Face pyramids OK.
    Max skewness = 0.714037 OK.
    Coupled point location match (average 0) OK.

Mesh OK.

And that's it. Basically dividing a shape into hexagonal (or pentagonal) volumes and using transfinite algorithm one can mesh anything with hexagons. Though when the number of entities in the geometry file increases usability of GUI goes down, it is still a little bit more convenient than blockMesh.